Teorema lui Thales din Milet, primul, al doilea și exemple

Primul și al doilea Teorema lui Thales din Milet ele se bazează pe determinarea triunghiurilor de la cele similare (prima teorema) sau circumferințele (teorema a doua). Ele au fost foarte utile în diferite domenii. De exemplu, prima teoremă sa dovedit a fi foarte utilă pentru măsurarea structurilor mari atunci când nu exista instrumente sofisticate de măsurare.

Thales a fost un matematician grec care a furnizat contribuții importante la geometria care evidențiază aceste două teoreme (în unele texte scrise, cât și ca Thales) și aplicații utile. Aceste rezultate au fost folosite pe parcursul istoriei și au permis rezolvarea unei mari varietăți de probleme geometrice.

index

• 1 Prima teoremă a poveștilor
  • 1.1 Aplicație
  • 1.2 Exemple
• 2 a doua teoremă a poveștilor
  • 2.1 Aplicație
  • 2.2 Exemplu
• 3 Referințe

Prima teoremă a Tales

Prima teoremă a Tales este un instrument foarte util care, printre altele, permite construirea unui triunghi asemănător cu altul, cunoscut anterior. Din aceasta sunt derivate diferite variante ale teoremei care pot fi aplicate în mai multe contexte.

Înainte de a vă da declarația, amintiți-vă câteva noțiuni de similitudine a triunghiurilor. În esență, două triunghiuri sunt similare în cazul în care unghiurile lor sunt congruente (au aceeași măsură). Acest lucru dă naștere faptului că, dacă două triunghiuri sunt similare, părțile lor (sau homologii) corespunzătoare sunt proporționale.

Prima teorema a lui Thales afirmă că, dacă într-un triunghi dat o linie dreaptă este trasată paralelă cu oricare dintre laturile sale, noul triunghi obținut va fi similar cu triunghiul inițial.

În figura precedentă, triunghiurile ABC și DEC sunt similare. Proporționalitatea obținută ca urmare a acestei asemănări dă naștere și unei relații de proporționalitate între două laturi ale aceluiași triunghi și cele două laturi corespunzătoare celeilalte. De exemplu, luând în considerare cifra anterioară, trebuie să:Un alt mod în care se poate vedea prima teoremă astfel, și este de asemenea util, este după cum urmează: în cazul în care două linii L1 și L2 (orice) sunt tăiate linii paralele (orice număr dintre acestea), apoi segmentele formate în L1 sunt proporționale cu cele corespunzătoare formate în L2.

De asemenea, veți obține o relație între unghiurile formate, după cum se vede în figura următoare.

cerere

Printre numeroasele sale aplicații evidențiază un interes deosebit și are de a face cu unul dintre modurile în care au fost făcute măsurători ale structurilor mari din cele mai vechi timpuri, timp în care a trăit Tales și în cazul în care nu au contat pe aparatele moderne de măsurare Acum există.

Se spune că Thales a reușit să măsoare cea mai înaltă piramidă din Egipt, Cheops. Pentru aceasta, Thales presupunea că reflexiile razelor solare au atins pământul, formând linii paralele. Sub această presupunere, el a blocat un vârf sau trestie verticală în pământ.

Apoi, el a folosit similaritatea celor două triunghiuri care rezultă, unul format de lungimea umbra piramidei (care poate fi calculată cu ușurință) și înălțimea piramidei (necunoscută), iar celălalt format de lungimi de umbră și înălțimea tijei (care poate fi, de asemenea, ușor de calculat).

Folosind proporționalitatea dintre aceste lungimi, puteți șterge și cunoaște înălțimea piramidei.

Deși această metodă de măsurare poate arunca o abordare semnificativă eroare în ceea ce privește precizia înălțimii și depinde de paralelismul razelor solare (care, la rândul său depinde de un timp precis), trebuie să recunoaștem că este o idee foarte inteligent și care a oferit o bună alternativă de măsurare pentru timp.

Exemple

Găsiți valoarea lui x în fiecare caz:

Primul caz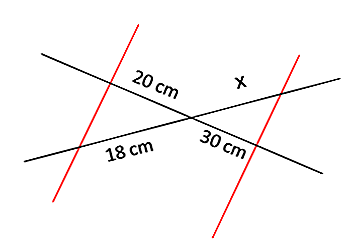 

soluție

Aici avem două linii tăiate cu două linii paralele. Prin prima teoremă a lui Thales se observă că părțile lor respective sunt proporționale. În special:

Cel de-al doilea caz

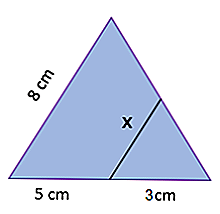
soluție

Aici avem două triunghiuri, una dintre ele formată de un segment paralel cu una dintre laturile celuilalt (tocmai partea laterală a lungimii x). Prin prima teoremă a Tales trebuie să:

A doua teoremă a Tales

A doua teorema a lui Thales determină un triunghi drept înscris pe o circumferință în fiecare punct al aceluiași.

Un triunghi inscripționat pe o circumferință este un triunghi al cărui vârfuri sunt pe circumferință, fiind astfel cuprins în aceasta.

In mod specific, a doua teoremă Astfel de stări de: dată o circumferință de centru O și diametrul AC, fiecare punct B din circumferința (altele decât A și C) determină un triunghi ABC cu unghi drept <>

Ca o justificare, rețineți că ambele OA și OB și OC corespund razei circumferinței; Prin urmare, măsurătorile lor sunt aceleași. De acolo se obtine ca triunghiurile OAB si OCB sunt isoscele, unde

Se știe că suma unghiurilor unui triunghi este egală cu 180 °. Folosind acest lucru cu triunghiul ABC trebuie:

2b + 2a = 180º.

În mod echivalent, avem b + a = 90º și b + a =

Rețineți că triunghiul drept furnizat de teorema a doua a lui Thales este tocmai a cărui ipoteuză este egală cu diametrul circumferinței.Prin urmare, este determinată complet de semicercul care conține punctele triunghiului; în acest caz, semicercul superior.

Rețineți, de asemenea, că în triunghiul drept obținut prin teorema a doua a lui Thales, hypotenuse este împărțit în două părți egale de OA și OC (raza). La rândul său, această măsură este egală cu segmentul OB (și raza), care corespunde mediei triunghiului ABC de către B.

Cu alte cuvinte, lungimea mediană a triunghiului drept ABC corespunzător vârfului B este complet determinată de jumătatea ipotezei. Amintiți-vă că mediana unui triunghi este segmentul de la unul dintre vârfuri până la jumătatea părții opuse; în acest caz, segmentul BO.

Circumferința circumscripționată

Un alt mod de a vedea a doua teorema lui Thales este printr-un cerc circumscris unui triunghi drept.

În general, un cerc circumscris unui poligon constă din circumferința care trece prin fiecare dintre vârfurile sale, ori de câte ori este posibilă urmărirea.

I folosind doua teoremă Un astfel dat un triunghi dreptunghic, putem construi întotdeauna o circumscris la aceasta, cu o rază egală cu jumătate din ipotenuza și circumscris (centrul cercului) ca mijlocul ipotenuzei.

cerere

O aplicație foarte importantă a doua teoremă astfel, și, probabil, cel mai utilizat, este de a găsi liniile tangente la o anumită circumferință, printr-un punct P extern la (cunoscută).

Rețineți că, având o circumferință (desenată în albastru în figura de mai jos) și un punct P exterior, există două tangente la circumferința trecerii prin P. Sean T și T „punctele de tangență, r raza cercului și Sau centrul.

Se știe că segmentul care merge de la centrul unui cerc până la un punct de tangență al acestuia este perpendicular pe această linie tangentă. Apoi, unghiul OTP este drept.

Din ceea ce am văzut mai devreme în prima teoremă despre Thales și versiunile sale diferite, vedem că este posibil să inscripționăm triunghiul OTP într-o altă circumferință (în roșu).

În mod analog, se obține că triunghiul OT'P poate fi inscripționat în aceeași circumferință anterioară.

Pentru a doua teoremă plus O astfel obținem noul diametrul cercului este tocmai ipotenuza triunghiului OTP (care este egal cu ipotenuza triunghiului OT'P), iar centrul este punctul median al acestui ipotenuzei.

Pentru a calcula centrul noului cerc suficient apoi calcula punctul de mijloc între circumferința centru spune M- inițial (deja cunoscute) și punctul P (de asemenea cunoscute). Apoi, raza va fi distanța dintre acest punct M și P.

Cu raza și centrul cercului roșu putem găsi ecuația carteziană, pe care ne-o amintim, dată de (x-h)² + (y-k)² = c², unde c este raza și punctul (h, k) este centrul cercului.

Cunoscând acum ecuațiile ambelor circumferințe, le putem intersecta prin rezolvarea sistemului de ecuații formate de acestea și obținând astfel punctele de tangență T și T '. În cele din urmă, pentru a cunoaște liniile tangente dorite, este suficient să găsim ecuația liniilor drepte care trec prin T și P și prin T 'și P.

exemplu

Luați în considerare o circumferință a diametrului AC, a centrului O și a unei raze de 1 cm. Fie B un punct pe circumferință astfel încât AB = AC. Cât măsoară AB?

soluție

Pentru a doua teoremă avem astfel de triunghi ABC este dreptunghi și ipotenuza corespunde diametrului, care în acest caz este de 2 cm (raza este de 1 cm). Apoi, prin teorema lui Pythagorean trebuie:

referințe

1. Ana Lira, P. J. (2006). Geometria și trigonometria. Zapopan, Jalisco: Edițiile pragului.
2. Goodman, A. și Hirsch, L. (1996). Algebra și trigonometria cu geometrie analitică. Pearson Education.
3. Gutiérrez, Á. Á. (2004). Metodologia și aplicațiile matematicii în E.S.O. Ministerul Educației.
4. IGER. (2014). Matematică Semestrul II Zaculeu. Guatemala: IGER.
5. José Jiménez, L. J. (2006). Matematică 2. Zapopan, Jalisco: Edițiile pragului.
6. M., S. (1997). Trigonometrie și geometrie analitică. Pearson Education.
7. Pérez, M. A. (2009). O istorie a matematicii: provocări și cuceriri prin caracterele lor. Cărți vizuale editoriale.
8. Viloria, N. și Leal, J. (2005). Geometrie analitică plană. Editorul Venezuelei C.