Transformări izometrice, tipuri și exemple
Transformări izometrice ele sunt modificări ale poziției sau orientării unei anumite figuri care nu modifică nici forma, nici mărimea acesteia. Aceste transformări sunt clasificate în trei tipuri: traducere, rotire și reflecție (izometrie). În general, transformările geometrice permit crearea unei figuri noi de la alta dată.
O transformare într-o figură geometrică înseamnă că, într-un fel, a fost supusă unei anumite schimbări; adică, că a fost modificată. Conform sensului originalului și similar în plan, transformările geometrice pot fi clasificate în trei tipuri: izometrice, izomorfe și anamorfe.

index
- 1 Caracteristici
- 2 tipuri
- 2.1 Prin traducere
- 2.2 Prin rotație
- 2.3 Prin reflecție sau simetrie
- 3 Compoziție
- 3.1 Componența unei traduceri
- 3.2 Componența unei rotații
- 3.3 Compoziția unei simetrii
- 4 Referințe
caracteristici
Transformările izometrice apar atunci când se păstrează magnitudinea segmentelor și unghiurile dintre figura originală și cea transformată.
În acest tip de transformare, nici forma, nici mărimea figurii nu sunt modificate (ele sunt congruente), este doar o schimbare a poziției figurii, fie în orientare, fie în direcție. În acest fel, cifrele inițiale și finale vor fi similare și geometric congruente.
Izometria se referă la egalitate; adică cifrele geometrice vor fi izometrice dacă au aceeași formă și dimensiune.
În transformările izometrice, singurul lucru care poate fi observat este o schimbare a poziției în plan, apare o mișcare rigidă, datorită căreia figura se schimbă de la o poziție inițială la o poziție finală. Această cifră se numește omoloagă (similară) cu originalul.
Există trei tipuri de mișcări care clasifică o transformare izometrică: traducerea, rotirea și reflexia sau simetria.
tip
Prin traducere
Sunt acele izometrii care permit să se miște în linie dreaptă toate punctele avionului într-o anumită direcție și distanță.
Atunci când o figură este transformată prin traducere, ea nu-și schimbă orientarea față de poziția inițială și nici nu își pierde măsurile interne, măsurarea unghiurilor și laturilor sale. Acest tip de deplasare este definit de trei parametri:
- O direcție, care poate fi orizontală, verticală sau oblică.
- Un sens, care poate fi la stânga, la dreapta, în sus sau în jos.
- Distanța sau magnitudinea, care este lungimea de la poziția inițială până la sfârșitul oricărui punct care se mișcă.
Pentru ca transformarea izometrică prin traducere să fie îndeplinită, ea trebuie să îndeplinească următoarele condiții:
- Figura trebuie să păstreze întotdeauna toate dimensiunile sale, atât liniare cât și unghiulare.
- cifra nu-și schimbă poziția față de axa orizontală; adică, unghiul său nu variază niciodată.
- Traducerile vor fi întotdeauna sintetizate într-un singur rând, indiferent de numărul de traduceri care sunt făcute.
Într-un plan în care centrul este un punct O, cu coordonate (0,0), traducerea este definită de un vector T (a, b), care indică deplasarea punctului inițial. Aceasta este:
P (x, y) + T (a, b) = P '(x + a, y + b)
De exemplu, dacă o traducere T (-4, 7) este aplicată la punctul de coordonate P (8, -2), obținem:
P (8, -2) + T (-4, 7) = P '[(8 + (-4)
În următoarea imagine (stânga) se poate observa modul în care punctul C a fost mutat până când a coincis cu D. A făcut acest lucru în direcția verticală, direcția a fost în sus și distanța sau magnitudinea CD-ului a fost de 8 metri. În imaginea corectă se observă traducerea unui triunghi:

Prin rotație
Ele sunt acele izometrii care permit cifrei să rotească toate punctele unui avion. Fiecare punct se rotește după un arc care are un unghi constant și un punct fix (centrul de rotație) determinat.
Aceasta înseamnă că orice rotire va fi definită de centrul de rotație și de unghiul de rotație. Atunci când o figură este transformată prin rotație, ea menține măsura unghiurilor și laturilor sale.
Rotirea are loc într-o anumită direcție, este pozitivă atunci când rotația este în sens contrar acelor de ceasornic (contrar modului în care mâinile ceasului se rotesc) și negativ când rotația este în sensul acelor de ceasornic.

Dacă un punct (x, y) este rotit în raport cu originea - adică, centrul său de rotație este (0,0) -, la un unghi de 90sau la 360sau Coordonatele punctelor vor fi:

În cazul în care rotația nu are un centru la origine, originea sistemului de coordonate trebuie să fie transferată la noua origine dată, pentru a putea roti cifra care are originea ca centru.
De exemplu, dacă o rotație de 90 este aplicată punctului P (-5,2)sau, în jurul originii și într-un sens pozitiv noile coordonate vor fi (-2,5).
Prin reflecție sau simetrie
Sunt acele transformări care inversează punctele și figurile avionului. Această investiție poate fi cu privire la un punct sau poate fi, de asemenea, cu privire la o linie.
Cu alte cuvinte, în acest tip de transformare fiecare punct al figurii originale este asociat cu un alt punct (imagine) al figurii omoloage, în așa fel încât punctul și imaginea sa să fie la aceeași distanță de o linie numită axa de simetrie .
Astfel, partea stângă a figurii va fi o reflectare a părții din dreapta, fără a schimba forma sau dimensiunile ei. Simetria transformă o figură în alta, deși în direcția opusă, așa cum se poate vedea în imaginea următoare:

Simetria este prezentă în multe aspecte, ca și în unele plante (floarea-soarelui), animale (păuni) și fenomene naturale (fulgi de zăpadă). Ființa umană o reflectă în fața lui, care este considerată ca un factor de frumusețe. Reflecția sau simetria pot fi de două tipuri:
Simetria centrală
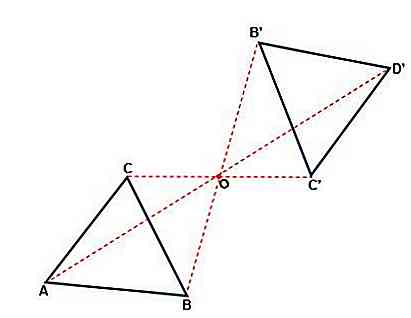
Este acea transformare care are loc cu privire la un punct, în care figura își poate schimba orientarea. Fiecare punct al figurii originale și al imaginii sale se află la aceeași distanță de un punct O, numit centrul simetriei. Simetria este centrală atunci când:
- Atât punctul, cât și imaginea și centrul aparțin aceleiași linii.
- Cu o rotație de 180sau din centrul O obțineți o cifră egală cu originalul.
- loviturile figurului inițial sunt paralele cu loviturile figurii formate.
- Sensul figurii nu se schimbă, va fi întotdeauna în sens orar.
 Simetrie axială
Simetrie axială
Această transformare are loc în raport cu axa simetriei, unde fiecare punct al figurii inițiale este asociat cu un alt punct al imaginii și acestea sunt la aceeași distanță față de axa simetriei. Simetria este axială atunci când:
- segmentul care unește un punct cu imaginea sa este perpendicular pe axa sa de simetrie;
- Cifrele schimbă direcția în raport cu rândul sau cu sensul acelor de ceasornic.
- Atunci când împărțiți cifra cu o linie centrală (axa simetriei), unul dintre jumătățile rezultate se potrivește complet cu una din jumătăți.

compoziție
O compoziție a transformărilor izometrice se referă la aplicarea succesivă a transformărilor izometrice pe aceeași figură.
Componența unei traduceri
Compoziția a două traduceri are ca rezultat o altă traducere. Când se realizează în plan, pe axa orizontală (x) se schimbă numai coordonatele acelei axe, în timp ce coordonatele axei verticale (y) rămân aceleași și invers.

Componența unei rotații
Compoziția a două rotații cu același centru are ca rezultat o altă rotire, care are același centru și a cărei amplitudine va fi suma amplitudinilor celor două rotații.
Dacă centrul turnurilor are un centru diferit, tăierea bisectorului a două segmente de puncte similare va fi centrul de rotație.

Compoziția unei simetrii
În acest caz, compoziția va depinde de modul în care este aplicată:
- Dacă aceeași simetrie este aplicată de două ori, rezultatul va fi o identitate.
- Dacă se aplică două simetrii în raport cu două axe paralele, rezultatul va fi o traducere, iar deplasarea este de două ori distanța dintre acele axe:

- Dacă două simetrii sunt aplicate în raport cu două axe care sunt tăiate în punctul O (centru), se va obține o rotație cu centrul la O și unghiul său va fi de două ori unghiul format de axe:

referințe
- V Burgués, J. F. (1988). Materiale pentru construirea geometriei. Madrid: Sinteza.
- Cesar Calavera, I. J. (2013). Desen tehnic II. Paraninfo S.A: Ediciones de la Torre.
- Coxeter, H. (1971). Bazele geometriei. Mexic: Limusa-Wiley.
- Coxford, A. (1971). Geometrie O abordare de transformare. SUA: Frații Laidlaw.
- Liliana Siñeriz, R. S. (2005). Inducție și formalizare în predarea transformărilor rigide în mediul CABRI.
- , P. J. (1996). Grupul de izometrii plane. Madrid: Sinteza.
- Suárez, A. C. (2010). Transformări în plan. Gurabo, Puerto Rico: AMCT.



 Simetrie axială
Simetrie axială